Example: Feedforward Networks
(예제 : 전방향 네트워크)
신경망을 사용하는데 있어서 우리의 목표는 가능한 빨리 오류를 최소화하는 지점에 도달하는 것이다. 우리는 트랙을 도는 경주를 하고 있는 중이고, 둥그런 고리의 같은 지점을 반복해서 지나고 있다. 경주의 시작 라인은 우리의 가중치가 초기화되는 상태이고, 결승 라인은 파라미터들이 정확한 분류와 예측을 할 수 있을 때의 상태이다.
경주 자체는 여러 단계를 포함하고 있고, 각 단계는 전후 단계가 유사하다. 달리기 주자처럼, 우리는 반복되는 행동을 되풀이하여 목표에 도달하게 될 것이다. 신경망에 대한 각 단계는 추측, 오류 측정, 계수를 증가시키는 수정과 같은 약간의 업데이트를 포함한다.
가중치의 모음은, 시작이나 끝의 상태와는 상관없이, 데이터 구조를 파악하기 위해 지상 검증 자료(ground-truth) 레이블과 데이터 모델 관계를 맺으려고 하기 때문에 모델이라고도 불린다. 모델은 일반적으로 나쁘게 시작해서 신경망이 변수들을 업데이트 하기 때문에 시간이 지남에 따라 결국 덜 나빠진다.
그 이유는 신경망이 무지에서 태어났기 때문이다. 신경망은 올바른 추측을 하기 위해 어느 가중치와 편향이 입력값을 가장 잘 변환하는지를 알지 못한다. 추측에서 시작해야만 하고, 실수에서 배움으로 점차적으로 더 좋은 추측을 시도하게 된다.(여러분은 신경망을 가설을 테스트하고, 다시 시도하는 과학적 방법의 아주 작은 실행으로 생각할 수 있다. 단지 눈가리개를 가지고 하는 과학적 방법일 뿐이다.)
여기 전방향 신경망을 통해 배우는 동안 무슨 일이 일어나는지에 대한 간단한 설명이 있다. 그것을 설명하기 위한 가장 간단한 아키텍처이다.
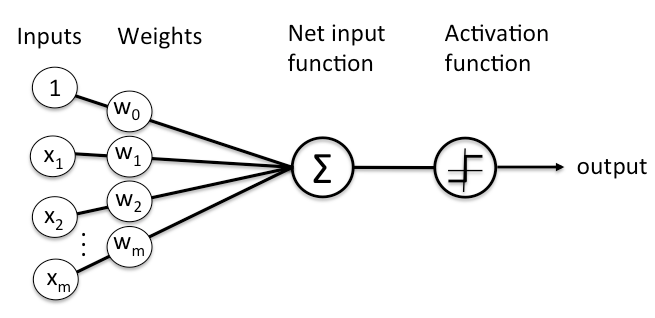
입력값이 네트워크로 들어간다. 계수나 가중치는 입력값을 네트워크가 마지막에 만들어 놓은 추측값들의 집합에 맵핑한다.
input(입력값) * weight(가중치) = guess(추측값)
가중치가 적용된 입력값은 그 입력값이 무엇인지 추측한 결과이다. 그런 다음 신경은 추측값을 받아서 데이터에 대한 지상 근거 자료(ground-truth)와 비교하고, 전문가에게 효율적으로 "제가 제대로 했나요?"하고 묻는다.
ground truth - guess = error
네트워크의 추측값과 지상 근거 자료(ground-truth)의 차이는 오류이다. 네트워크는 오류를 측정하고, 오류에 기여한 정도에 따라 가중치를 조정하여 모델에 반영하여 오류를 없앤다.
error(오류) * weight's contribution to error(가중치의 오류 기여도) = adjustment(조정값)
위의 3가지 의사 수학 공식은 3단계의 프로세스를 다시 시작하기 위한 신경망의 세가지 주요 기능(입력값 점수 산정:scoring input, 손실 계산:calculating loss, 모델 업데이트 적용:applying an update to the model)을 설명하고 있다. 신경망은 올바른 추측값을 지원하는 가중치를 보상히고, 오류를 이끌어 내는 가중치를 처벌하는 올바른 피드백 고리이다.
위의 첫번째 단계를 더 깊이 들어가 보자.
Multiple Linear Regression
(다중 선형 회귀)
생물학적으로 영감을 얻은 이름에도 불구하고, 인공신경망은 다른 머신러닝 알고리즘처럼 수학과 코드에 불과하다. 사실은, 통계학에서 배우는 첫번째 방법 중 하나인 선형 회귀를 이해하는 누구라도, 신경망이 어떻게 동작하는지를 이해할 수 있다. 가장 간단한 형태로, 선형 회귀는 다음과 같이 표현된다.
여기서 Y_hat은 추정된 출력값이고, X는 입력값, b는 기울기, a는 2차원 그래프에서 수직 축에 대한 절편이다.(이것을 더 구체적으로 하자면, X는 방사선 피폭, Y는 암 위험도가 될 수 있다. 또는 X는 매일 하는 엎드려 팔굽혀펴기, Y는 벤치프레스-벤치에 누워 역기 들어올리는 운동- 총무게일 수 있다. 또는 X는 비료의 양, Y는 농작물의 크기일 수도 있다.) X축에서 얼마나 멀리 떨어져 있는지에 상관없이, X에 단위를 추가할 때마다, 종속 변수 Y는 비례하여 커진다는 것을 상상할 수 있다. 서로 위 아래로 움직이는 2개의 변수 사이의 단순한 관계가 시작점이다.
다음 단계는 여러 개의 입력값으로 출력값을 생성하는 다중 선형 회귀를 생각해 보는 것이다. 일반적으로 다음과 같이 표현된다.
Y_hat = b_1*X_1 + b_2*X_2 + b_3*X_3 + a
(위의 수확량 예제를 확장하기 위해서, 비료 변수에 성장기의 햇빛의 양과 강우량을 추가하고, 3가지 모두 Y_hat에 영향을 줄 수 있다.)
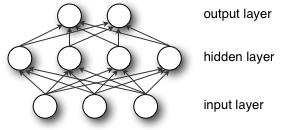
이제 다중 선형 회귀의 형태가 신경망의 모든 노드에서 발생한다. 단일 계층의 각 노드에서, 이전 계층의 각 노드로부터의 입력은 모든 다른 노드의 입력값과 재결합된다. 즉, 입력값들이 각자의 계수에 따라 다른 비율로 섞이고, 후속 계층의 각 노드로 다르게 이어진다. 이러한 방식으로, 망에서 오류를 줄이기 위해서 입력의 조합이 중요하다는 것에 대한 테스트를 수행한다.
노드의 입력값들을 합해서 Y_hat에 도달하면, 비선형 함수를 통과하게 된다. 이유는 여기에 있다 : 만약 모든 노드가 단지 다중 선형 회귀를 수행한다면, Y_hat은 선형으로 증가하고 X의 증가에 따른 제한이 없다. 그러나, 그것은 우리의 목적에 부합하지 않는다.
각 노드에서 우리가 만들고자 하는 것은 입력 신호가 통과하여 궁극적으로 네트워크의 결정에 영향을 미치는지의 여부에 따라 켜지고 꺼지는 스위치(뉴런과 같은...)이다.
스위치가 있을 때, 분류 문제가 있다. 입력 신호가 노드가 충분히 분류했는지 아닌지, On인지 Off인지를 지시하는가? 2진 결정은 1과 0으로 표현될 수 있다. 그리고 로지스틱 회귀는 0과 1사이의 공간으로 변형하기 위해 입력값을 축소하여 밀어넣는 비선형 함수이다.
각 노드에서 비선형 변환은 일반적으로 로지스틱 회귀와 유사한 s-shaped 함수들이다. 그 함수들은 sigmoid(그리스어 단어 "S"), tanh, hard tanh 등으로 가고, 각 노드의 출력값을 형성한다. 0과 1사이의 s-shaped 공간에 각각 밀어넣어진 모든 노드의 출력값은 전방향 신경망에서 다음 레이어의 입력값으로 전달되고, 신호가 결정이 내려지는 네트워크의 마지막 레이어에 도달할 때까지 계속된다.
트랙백 주소 :: http://www.yongbi.net/trackback/790
트랙백 RSS :: http://www.yongbi.net/rss/trackback/790



댓글을 달아 주세요
댓글 RSS 주소 : http://www.yongbi.net/rss/comment/792