(로지스틱 회귀 : 독립변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용디는 통계 기법, 확률 모델. 로지스틱 회귀의 목적은 일반적인 회귀 분석의 목표와 동일하게 종속 변수와 독립 변수간의 관계를 구체적인 함수로 나타내어 향후 예측 모델에 사용하는 것이다.)
많은 레이어를 가진 심층 신경 네트워크(deep neural network)에서 마지막 레이어는 특별한 역할을 갖는다. 레이블이 지정된 입력을 처리할 때, 마지막 출력 레이어는 가장 가능성 있는 레이블을 적용하여 각 예제를 분류한다. 출력 레이어의 각 노드는 하나의 레이블을 나타내고, 노드는 이전 레이어의 입력과 파라미터로부터 수신한 신호의 강도에 따라 켜지거나 꺼진다.
각 출력 노드는 입력 변수가 레이블을 가질 가지가 있거나 없기 때문에 이진 출력값 0과 1의 2개의 가능한 결과를 생성한다. 어쨌든, 약간의 잉태같은 것은 없다.
레이블이 지정된 데이터로 작업하는 신경망(neural network)은 2진 출력을 생성하지만, 신경망이 받는 입력은 종종 연속적이다. 즉, 네트워크가 입력으로 수신하는 신호는 값들의 범위에 걸쳐 이어져 있고 해결하고자 하는 문제에 따라 많은 수의 메트릭(기준)을 포함하고 있다.
예를 들어, 추천 엔진은 광고를 게재할 것인지 아닌지에 대해 2진 결정을 내려야만 한다. 그러나, 그 결정의 기반이 되는 입력은 지난 주 얼마나 많은 고객이 Amazon에서 시간을 보냈는지, 혹은 고객이 해당 사이트를 얼마나 자주 방문했는지를 포함하고 있다.
따라서 출력 레이어는 기저귀에 67.59달러를 썼고, 웹 사이트에 15회 방문했다는 것과 같은 신호를 0과 1 사이에서 압축을 해야만 한다. 즉, 주어진 입력이 레이블이 붙여져야 하는지 아닌지의 확률을 계산해야 한다.
지속적인 신호를 이진 출력으로 변환하는데 사용하는 메커니즘을 로지스틱 회귀라고 한다. 불행하게도 로지스틱 회귀라는 이름은 대부분의 사람들이 친숙한 선형 의미에서의 회귀 분석보다는 분류를 위해 사용된다. 입력값들의 집합이 레이블에 일치할 확률을 계산한다.
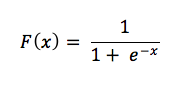
이 작은 수식을 살펴보자.
확률로 표시되는 연속되는 입력의 경우, 음의 확률같은 것이 없기 때문에 양의 결과를 출력해야만 한다. 그래서 출력이 0보다 커야 하기 때문에 분모는 e의 지수가 된다. 이제 e의 지수와 분수 1/1 사이의 관계를 고려해 보자. 알다시피 1은 확률의 결과가 터무니없지 않고는 넘어갈 수 없는 한도이다. (120%로 확신한다.)
레이블을 작동시키는 입력값 x가 증가함에 따라 x에 대한 e의 표현은 0으로 줄어들어서 분수 1/1이나 100%로 남게 된다. 이것은 (언제고 상당히 접근하는 것이 아니라) 레이블에 적용되는 절대 확실성에 도달함을 의미한다. 출력과 음의 상관관계가 있는 입력은 e의 지수에 음수 부호로 뒤집힌 값을 가지게 되고, 음수 신호가 커지면 x에 대한 e의 양이 커져서 전체 분수는 0에 가까워지게 된다.
이제 x를 지수로 갖는 것보다 모든 가중치와 해당 입력값들의 곱을 합한 것, 즉 네트워크를 통과하는 모든 신호를 상상해 보자. 그것이 신경망 분류기(neural network classfier)의 출력 레이어에서 로지스틱 회귀 레이어로 반영되는 것이다.
이 레이어를 사용하면, 위에는 예를 1로 레이블을 지정하고, 아래에는 표시하지 않는 임계값을 결정하여 설정할 수 있다. 원하는 대로 임계값을 다르게 설정할 수 있다. 오류를 어느 쪽에 적용할 것인지에 따라 낮은 임계값은 거짓 양성(false positive:통계상 실제로는 음성인데 검사 결과는 양성이라고 나오는 것, 위양성 혹은 거짓 정보)을 증기시키고, 높은 임계값은 거짓 음성(false negative:통계상 실제로는 양성인데 검사 결과는 음성이라고 나오는 것. 2종 오류. 거짓 양성보다 오탐 비용이 커짐.)을 증가시킨다.



댓글을 달아 주세요
댓글 RSS 주소 : http://www.yongbi.net/rss/comment/793